Readers Question: When my class and I try to test the Marshall-Lerner condition it doesn’t always work. i.e. we assumed a country with just one export and one import and assumed their price elasticities added up to less than one. We gave each a price and quantity that led to a current account balance =0 for simplicity then assumed a devaluation of the exchange rate – on calculating the new quantities and then new current account balance IT IMPROVED. Why ? I can give the figures we worked with if that helps…or does the Marshall-Lerner condition have additional conditions?
To be honest, I have never tested the Marshall Lerner condition with figures. I have always just taught it as given that what is in the textbooks must be correct. There is probably some mathematical proof that the Marshall Lerner condition must hold. But, to be honest, I don’t know it. (it isn’t required for what I teach) I think the most likely thing is an error in your calculation.
Definition of The Marshall Lerner condition
This states that, for a currency devaluation to lead to an improvement (e.g reduction in deficit) in the current account, the sum of price elasticity of exports and imports (in absolute value) must be greater than 1.
- E.g. if PED of exports is -0.2
- And if PED of Imports is -0.5
In this case, a devaluation of the currency should worsen the current account.
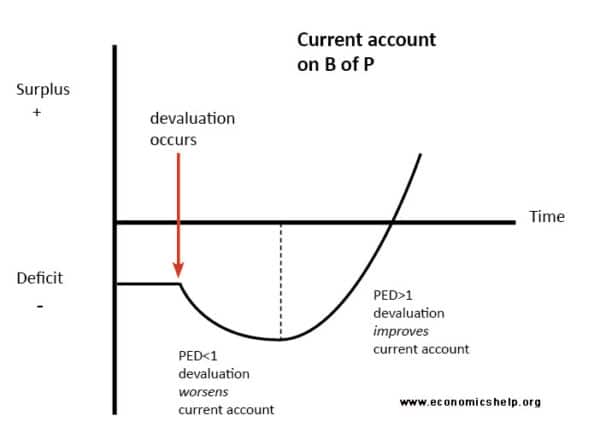
Empirical evidence suggests the elasticity of demand for exports and imports tends to be inelastic in the short run, but more elastic in the long run. Therefore a devaluation often worsens the current account in the short term but improves it in the long-term
(in absolute value means modulate numbers.) i.e. -0.3 + -0.6 = 0.9

can you please show the working with the numbers?otherwise i’m not sure about where exactly went wrong..anyway,just thought of an important assumption that the trade balance STARTED even,i.e.M(expenditure)=p(international price)*X(export volume).
There are two common errors which make ML calculations incorrect:
1. The ML condition assumes that we start with a balanced trade position, i.e. that the value of imports equals the value of exports.
2. It is sometimes assumed that following a depreciation, the price received by the exporter falls. This is erroneous. If the exchange rate is £1 = $2, then an exporter who sells a product for £1 will receive £1, but the American purchaser will pay $2. If the exchange rate falls to £1 = £1.80, a 10% depreciation, an exporter selling a product for £1 will STILL receive £1, but the American purchase will now only have to pay $1.80. As the price appears to the American to be lower, they should be persuaded to increase their demand, depending on their sensitivity to a change in price.
WORKED EXAMPLE
Exchange Rate £1 = $2
Exports
Price Demand Revenue
£100 500 £50 000
Imports
Price Demand Revenue
£50 1000 £50 000
Trade balance = £0
After Depreciation
Exchange rate £1 = $1.80 – a depreciation of 10%
1. M-L condition NOT satisfied
PED (X) + PED (M) 1
0.6 + 0.8 = 1.4
After depreciation:
Exports
Price Demand Revenue
£100 520 £53 000
Imports
Price Demand Revenue
£55 920 £50 600
Trade balance = £2 400
As the M-L condition IS satisfied, a depreciation of the currency leads to an improvement in the trade balance.
Ny first post lost some information in the middle – is this a space issue?
There are two common errors which make ML calculations incorrect:
1. The ML condition assumes that we start with a balanced trade position, i.e. that the value of imports equals the value of exports.
2. It is sometimes assumed that following a depreciation, the price received by the exporter falls. This is erroneous. If the exchange rate is £1 = $2, then an exporter who sells a product for £1 will receive £1, but the American purchaser will pay $2. If the exchange rate falls to £1 = £1.80, a 10% depreciation, an exporter selling a product for £1 will STILL receive £1, but the American purchase will now only have to pay $1.80. As the price appears to the American to be lower, they should be persuaded to increase their demand, depending on their sensitivity to a change in price.
WORKED EXAMPLE
Exchange Rate £1 = $2
Exports
Price Demand Revenue
£100 500 £50 000
Imports
Price Demand Revenue
£50 1000 £50 000
Trade balance = £0
After Depreciation
Exchange rate £1 = $1.80 – a depreciation of 10%
1. M-L condition NOT satisfied
PED (X) + PED (M) 1
0.6 + 0.8 = 1.4
After depreciation:
Exports
Price Demand Revenue
£100 520 £53 000
Imports
Price Demand Revenue
£55 920 £50 600
Trade balance = £2 400
As the M-L condition IS satisfied, a depreciation of the currency leads to an improvement in the trade balance.
This section keeps being omitted:
1. M-L condition NOT satisfied
PED (X) + PED (M) < 1
0.4 + 0.5 = 0.9
After depreciation:
Exports
Price Demand Revenue
£100 520 £52 000
Imports
Price Demand Revenue
£55 950 £52 250
Trade balance = (£250)
As the M-L condition is not satisfied, a depreciation of the currency leads to a worsening of the trade balance.
Thank you for giving this explanation. There’s an small error in the calculation: 6% of 500 is 30, not 20 as shown.
Thanks Paul
Hello,
please, could you explain me, how to calculate Marshall-Lerner condition for a country? Could you give me the exact formula? I am not sure, how to do it, which data to use – if I calculate ML in a year, do I use average exchange rate? etc.
I would really appreciate any help. Thank you and than you once again!
how will you calculate price elasticity of demand for export and import individually?
can you help me with the following question:
exchange rate $1=E 0.5
export Q(demand) Price revenue
100 E 1 100
import 40 $5 200
exchange rate $1= E 2/3
Q(demand) Price revenue
exp 105 E 1 105
imp 36 $ 5 180
thanks for explanation. Now i can find out the effects of devaluation