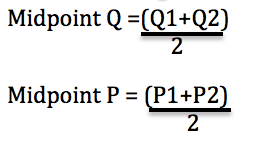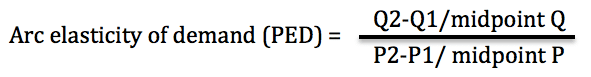Definition: Arc elasticity of demand measures elasticity between two points on a curve – using a mid-point between the two curves.
On most curves, the elasticity of a curve varies depending on where you are. Therefore elasticity needs to measure a certain sector of the curve.
Calculating Arc Elasticity of Demand
To calculate arc elasticity of demand we first take the midpoint in between.
Once we have the midpoint, we calculate the PED in the usual way
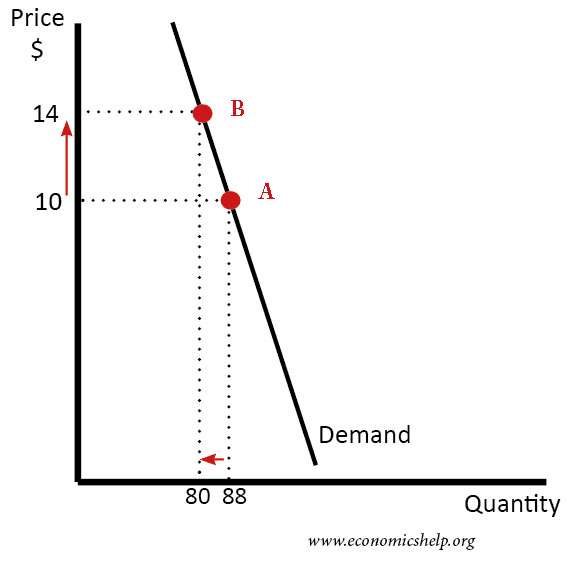
Example of calculating Arc Elasticity of Demand
- The mid point of Q = (80+88)/2 = 84
- The mid-point of P =(10+14)/2 =12
- % change in Q = 88-80/84 = -0.09524
- % change in price = (14-10)/12 = 0.3333
- PED = -0.09524 /0.3333 = -0.28571
Comparison with measuring elasticity as point A to B
If we calculated elasticity from point A to B. We would take the starting point as the reference.
- The % change in Q would be 8/88 = 0.90909
- The % change in Price would be 4/10 = -40
- Therefore PED would be 0.90909/-40 = -0.22727
Example 2
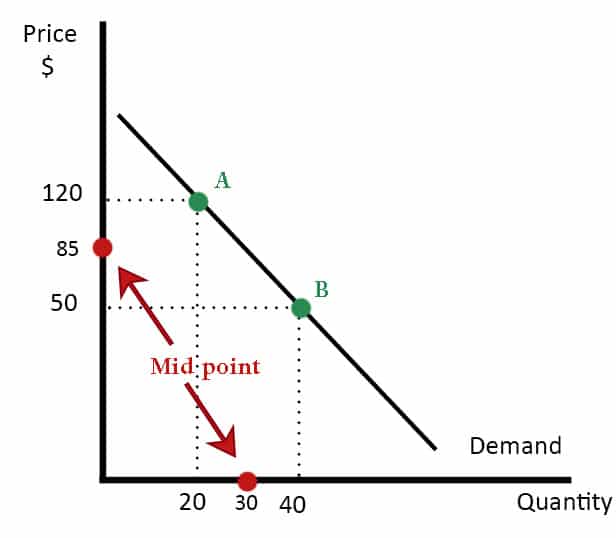
Quantity has fallen from 40 to 20 (change in quantity of 20)
Using arc-elasticity of demand
PED =
Change in Q (20) /midpoint (30) = – 0.66666
Change in p (70) /midpoint (85) = 0.823529
PED = – 0.809
If we calculated PED from points B to A.
% change in QD would be 20/40 (50%
% change in price would be 70/50 (140%)
PED = -0.35
If we calculated PED from points A to B
% change in QD would be 20/20 (100%)
% change in price would be 70/120 (58%)
PED = -1.72
Formula for Average or ‘midpoint’ elasticity of demand
(change in Q / average Q )
—————————
(change in P / average P)