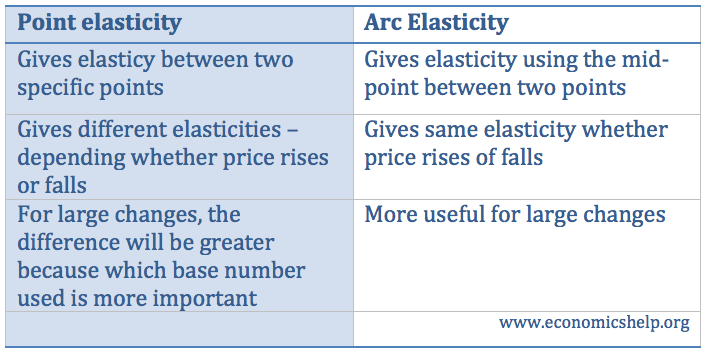
When calculating elasticity of demand there are two possible ways.
- Point elasticity of demand takes the elasticity of demand at a particular point on a curve (or between two points)
- Arc elasticity measures elasticity at the midpoint between the two selected points:
Formula for point elasticity of demand is:
PED =
% Δ Q / Q
————-
% Δ P / P
To get more precision, you can use calculus and measure an infinitesimal change in Q and Price ( where ð = very small change) This is the slope of the demand curve at that particular point in time.
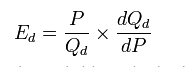
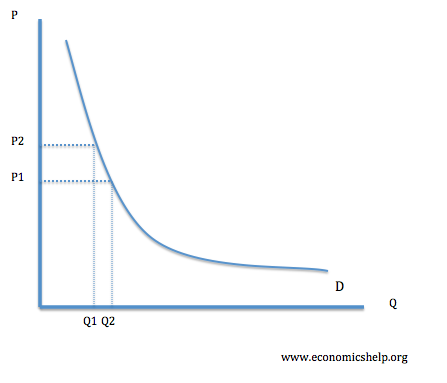
Arc Elasticity
Arc elasticity measures the mid point between the two selected points:
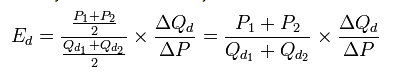
Example of Difference between Point and Arc Elasticity A to B
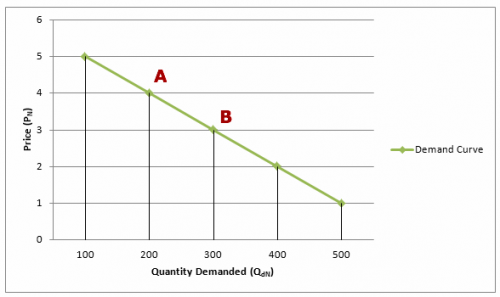
Point elasticity A to B
- Quantity increase from 200 to 300 = 100/200 = 50%
- Price falls from 4 to 3 = 1/4 = -25%
- Therefore PED = 50/ -25 = – 2.0
Mid Point (Arc) Elasticity A to B
- Mid point of Q = (200+300) / 2 = 250
- Mid Point of P = (3+4) / 2 = 3.5
- Q % = (100/250) = 40%
- P % = 1/3.5 = 28.57
- PED = 40/-28.57 = – 1.4
(or ( 3.5/250) * 100/1 = – 1.4)
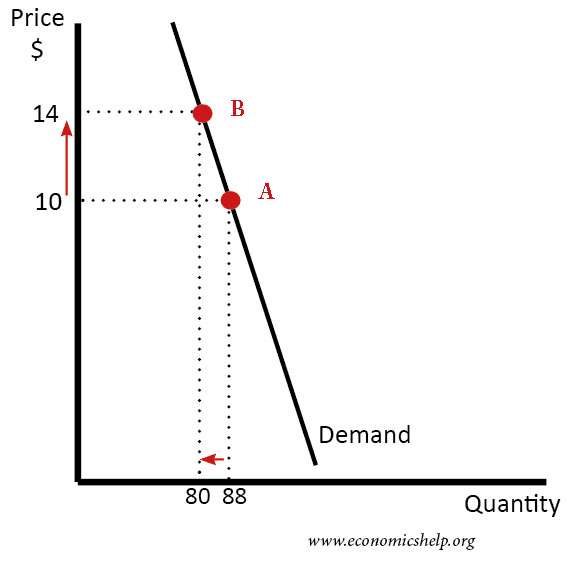
Example of calculating Arc Elasticity of Demand
Arc ‘mid-point’ elasticity
- The mid point of Q = (80+88)/2 = 84
- The mid-point of P =(10+14)/2 =12
- % change in Q = 88-80/84 = -0.09524
- % change in price = (14-10)/12 = 0.3333
- PED = 0.333/-0.9524 = -0.285
Comparison with measuring elasticity as point A to B
If we calculated elasticity from point A to B. We would take the starting point as the reference.
- The % change in Q would be 8/88 = 10%
- The % change in Price would be 4/10 = -40%
- Therefore PED would be 10/-40 = -0.25
Example 2
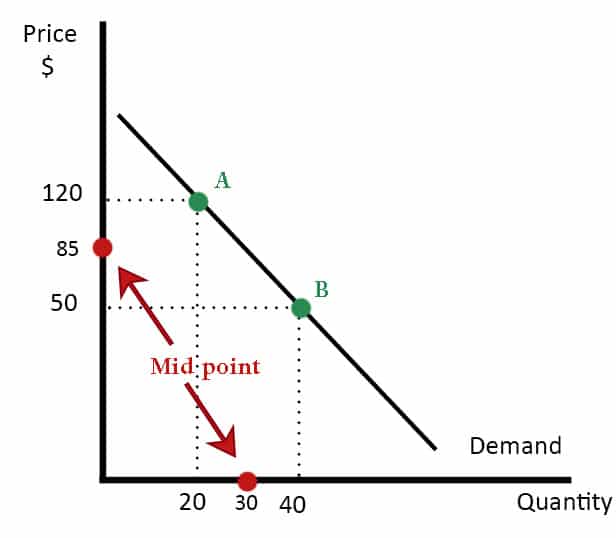
Quantity has fallen from 40 to 20 (change in quantity of 20)
Using arc-elasticity of demand
PED =
Change in Q (20) /midpoint (30) = – 0.66666
Change in p (70) /midpoint (85) = 0.823529
PED = – 0.809
If we calculated PED from points B to A.
% change in QD would be 20/40 (50%
% change in price would be 70/50 (140%)
PED = -0.35
If we calculated PED from points A to B
% change in QD would be 20/20 (100%)
% change in price would be 70/120 (58%)
PED = -1.72
Readers Question: I wonder if you could possibly help with the problem we encountered when we’re trying to calculate PED and a change in Total Revenue in a random example.
By taking random numbers we have found ourselves in a situation where TR has not increased when the price increased, given that D was price inelastic.The figures are as follows:
- Price increased from 10-20, (10/10 = 100% increase in price)
- QD had fallen from 10-5 units. (5/10 = 50% fall in price
- Surely, it gives PED of -0.5? – yes using PED
This suggests that D is price inelastic, hence TR should have increased. But it did not. Before the price was raised it equalled: 10×10=100 and after the rise in price: 20×5=100. It remained constant. Could you possibly explain why this has occurred?
All textbooks say that TR should increase when P is raised and D is price inelastic. It should work for any numbers as we can draw a demand curve through these two points (whether a straight line or hyperbolic). Does this imply that if demand is price inelastic and P rises TR may EITHER increase or stay the same or is there a much-complicated answer?
Using Arc elasticity of demand
we get a different elasticity of demand
Firstly we find the midpoint of Q and P. For Q This is (10+20)/2. For P this is 1(0+5)/2 = 7.5
- QD = 10/15 = 66% increase in quantity
- Price = 5/7.5 = 66% fall in price.
Therefore PED = 66/66 = 1.0 This explains why the revenue remained the same.
Elasticity and Revenue
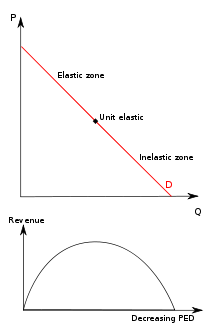
The thing with a straight line is that the elasticity varies. At the top left, quantity is showing a big % increase, compared to price.
Therefore, it makes a big difference whether we use point elasticity of arc elasticity.
Unitary Elasticity
This will be a rectangular hyperbola
With this shape, the % change is constant.
Note for A Level Students
It is not needed to know the difference between point and arc elasticity. I teach just point elasticity. That is why your calculations were correct. But, outcome confusing.
Related

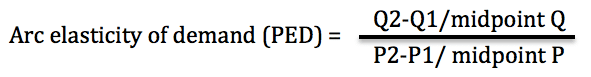
good material for studying
The example with 0.35 is incorrect the person got confused with the quantity and price.
Thanks Jonzen, have corrected.
thank you
it was very useful for me
i hope to be more explanation of other economic topics
Dear Tejvan Pettinger
I really must express my gratitude for the help you freely gave me to pass my Economics class. I realize how busy you are and know that it took a lot of time to get me ready for the test. I know I was on the verge of failing the class, and I could not get my head around the language at all. Your patience was much appreciated, and it is through your help that I have managed to pass the class with one of the best marks.
You are the sort of family friend that anyone would love.
Sincerely,
Melusi Ntombela
South Africa, University of Zululand
Very useful site, thank you so much. Has helped me
If Q=aP+b (a < 0), then we can prove that PED = P1 / (P1 + b/a) = constant, independent from P2.
Very useful this information.Thanks to writer.
thanks to writer😊…the article helps me in my studies
Hey,
While the write up helped me understand the concept, it still couldn’t help me find the answer to the original Q which I had posed to Google, which is “When do I use Arc Elasticity and when do I use point Elasticity for calculation, especially since both the answers are different.”. Any help on this topic would be deeply appreciated.
Also, thanks for the write up. It is people like you and your work which is making my life easier as a student after having a break of more than a decade.
Plz help me for solving my question of Economics. I am a new student of Economics did my best to solve them but failed. I would request to assist me for my tomorrow assignment.
1. Calculate price elasticity by using point elasticity method when the company is in state of equilibrium and interpret the result.
2. What will happen to supply of cement equilibrium price and equilibrium quantity of cement if government gives subsidy to cement manufacturers?
Thanks
Sani from Pakistan
Really helpful site
thanks for your the response