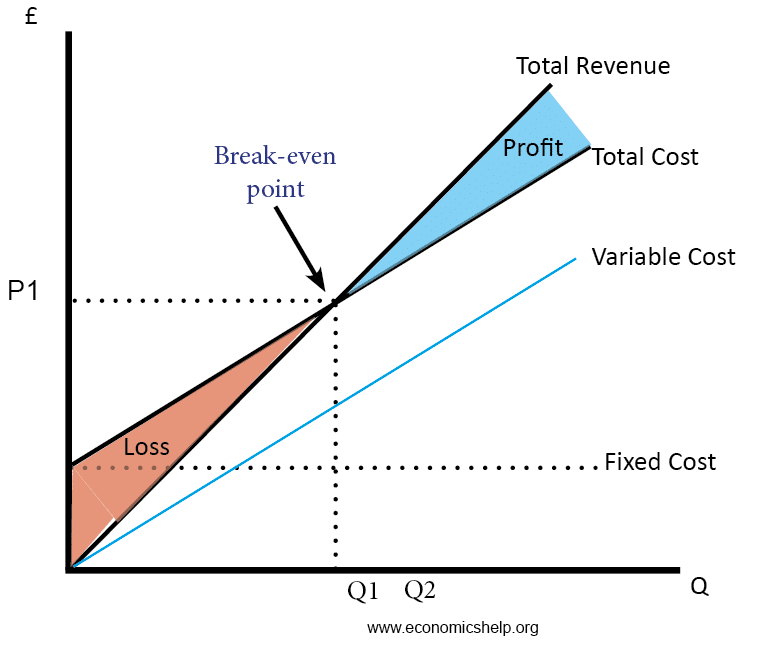
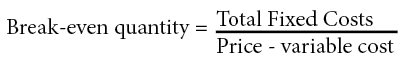The break-even price is the price necessary to make normal profit. It is a price which includes all costs, including variable and fixed costs.
- At the break-even price, the firm neither makes a loss or profit.
- The break-even price occurs where AR = ATC
- The break-even price occurs where Total Revenue = Total Cost (TC)
Formula for break-even price
(Total fixed cost / production unit volume) + variable cost per unit
Example of break-even price calculation
- Fixed costs = £12,000
- Average variable cost = £12
- Output = 3,000
- Break-even price = (12,000/3,000) + £12 = £16
Example 2
- If the output increases to 24,000, the break-even price would be lower.
- The average fixed cost would now be 12,000/24,000) = £0.50
- Therefore, the break-even price would be £12.50
Diagram of break-even price
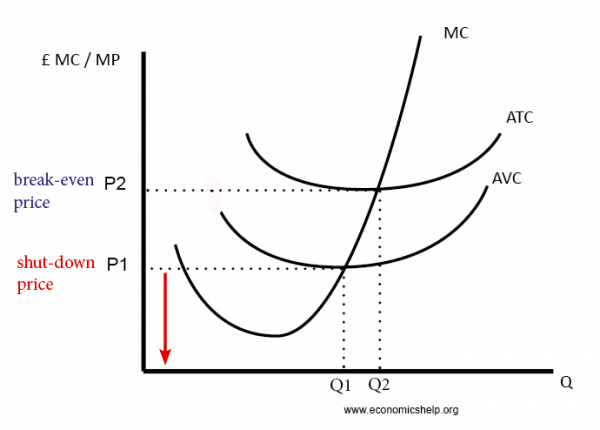
At P2 – average revenue (AR) = ATC.
Break-even output
Suppose:
- Fixed costs = £40,000
- Average variable cost = £8
- Market Price = £13
How much does the firm need to sell in order to break even, with a market price of £13?
Q = 40,000/ (13-8)
Q = 8,000
Uses of break-even price
- A firm will be interested to know the break-even price. For example, if it is entering a market, it may be interested in the lowest price it can set without making a loss.
- This is important for a firm with the objective of sales maximisation. One definition of sales maximisation is setting the price as low as possible, whilst still making normal profit (and breaking even).
- A firm may find out its break-even price and then add a certain profit margin, to help set prices.
Evaluation of break-even price
- A firm may not be able to easily calculate all its average total costs, and so in the real world, it could get the price wrong.
- Similarly, it may calculate break-even price on a certain output, but if demand is less than expected, the price will be too low.
Related