A zero-sum game is a situation where one party benefits at the equal cost of another. If we add gains and losses the net benefit will always be zero.
- If two players have an arm wrestle challenge, there can only be one winner and one loser. It is not possible to arm wrestle and both to win. I win – you lose. This is a zero-sum game.
- If I take three apples from you. You have lost three; I have gained three. There is the same overall number of apples, just a redistribution of who owns them. This is a zero-sum game.
Zero-sum games in economics
In economics, there are quite a few examples of zero-sum games.
- Licensing rights. If the government give a right to mine natural resources to one company, it is at the expense of a rival company who is not able to mine.
- Insurance payouts. If an insurance company agrees to pay out for a loss of property, you gain and they lose. They transfer $1,000 from their account to yours.
- Future and options contracts. These are agreements where depending on changes in prices, investors will transfer wealth to another investor.
- Distribution of budget. If the government has $100bn to spend between education and health care, increasing the budget for health care, means less spending for education. (* though this isn’t necessarily a zero-sum game, see below)
- Current account deficit. If there are two countries, and one runs a current account surplus, the other country must run an equivalent current account deficit, by definition.
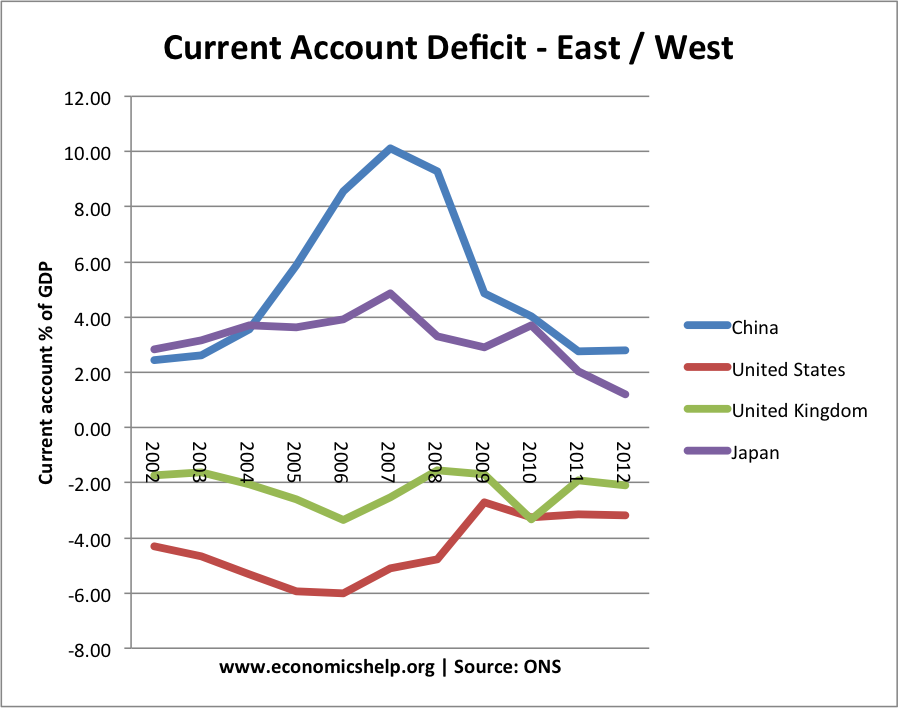
This shows a rough inverse relationship between China and US current account deficit. As US deficit increases, Chinese surplus also increases.
Production Possibility Frontier and Zero-sum game
Zero-sum game theory
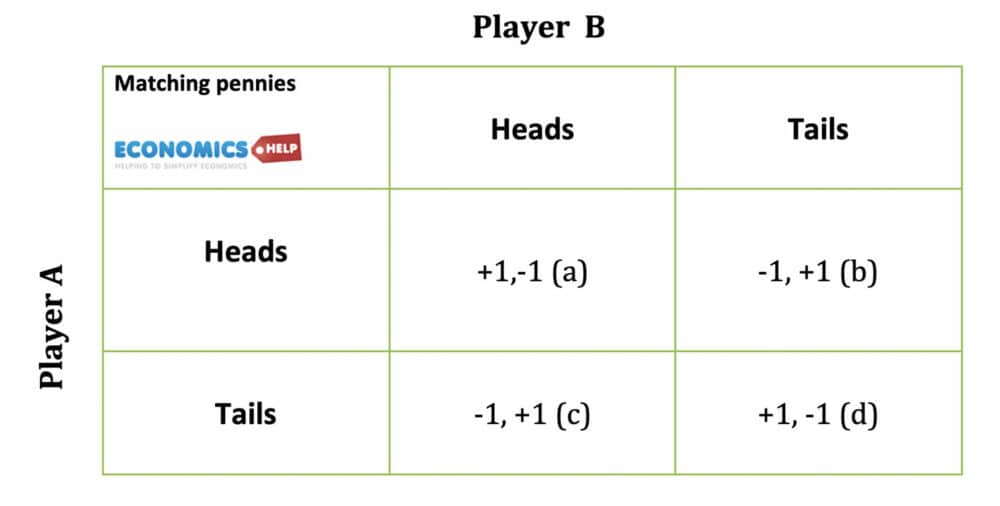
Matching Pennies Game
- This is a game with two players. They both put a penny on the table.
- If the pennies are Heads/heads or tails/tails – then Player A wins both pennies. He gains 1, (player B loses 1)
- If the pennies are mixed (heads/tails) or tails/heads then play B wins both pennies.
Entering or leaving the market
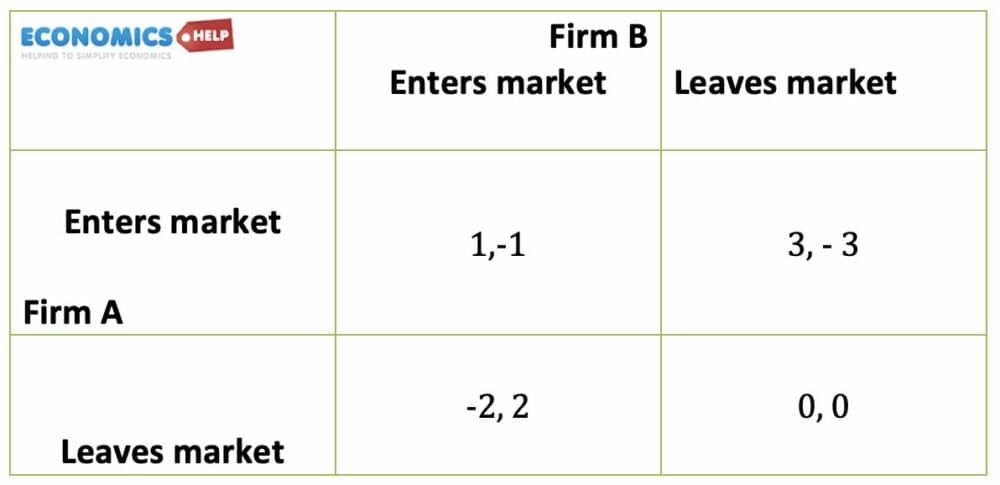
The dominant strategy for both firms is Firm A enters the market. Firm B enters the market, so we end up at top left (1,-1) Which means firm A is benefiting at the expense of firm B.
Non-zero sum game
In a non-zero-sum game, it is possible for two parties to both benefit from a decision. For example, if Portugal and the UK engage in free trade, both countries can see a rise in economic welfare. Most transactions are non-zero-sum games because most transactions can be beneficial to both.
Prisoners dilemma
The prisoner’s dilemma is a non-zero sum game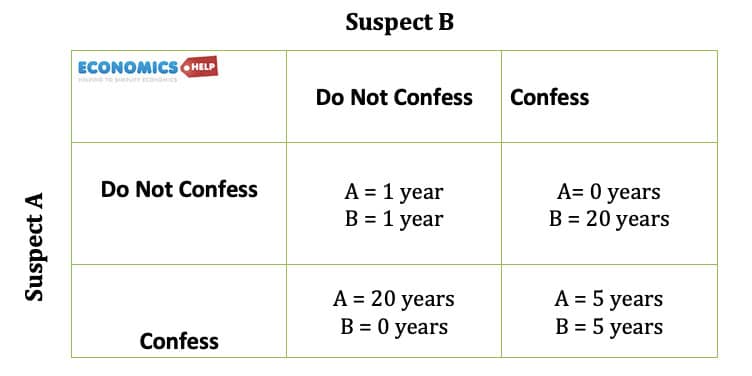
In this case, by both colluding and agreeing not to co-operate, both parties can benefit
Zero-Sum of Mercantilism vs Free Trade
Mercantilism is an economic theory, which generally saw economic prosperity as a zero-sum game. Before the nineteenth century, many believed that the key to improving economic welfare was to take natural resources from others, run a trade surplus and accumulate gold/silver. It was all based on the concept that economic resources were limited and therefore if you wanted to become better off, you needed to take it before other people did. This zero-sum game approach had very important political implications. It was a motivation behind the ‘age of empire’. European countries sought to gain natural resources from other countries around the world. This led to the formation of Empire building and claiming natural resources from other countries.
In the nineteenth century, economists increasingly questioned this zero-sum game approach. Adam Smith in the Wealth of Nations, sought to show how people could pursue their own self-interest and become better off – but, importantly, other people could also become better off. Commerce was not a zero-sum game, because if firms develop new products and expand, they pay workers more, and ultimately workers can buy more goods.
In the case of free trade, David Ricardo sought to prove that free trade was a way for both countries to become better off. By specialising in their areas of comparative advantage they could enjoy higher living standards through specialisation and trade. This had important political implications because it encouraged a belief that empire building and conquest was not the route to prosperity. Countries could freely trade and both become better off.
‘China taking US jobs’
Under Trump, there was a claim that China was taking US jobs. The observation is that by running an undervalued currency and a current account surplus, China was artificially making exports more competitive. Therefore, US jobs went to China and the US lost out.
It is not actually as clear cut as this view. The US was benefitting from cheaper consumer goods, which increased disposable income and led to greater demand and more US jobs elsewhere. Also, when China runs a trade surplus, it may seem like China is accumulating at the expense of the US. But, China uses its current account surplus to buy US bonds, keep US interest rates lower and so we cannot say it was a zero-sum game. But the interesting thing is it could be perceived as zero-sum game.
Dutch Disease
‘Dutch Disease‘ This is the observation that a sudden surge in one industry (oil and gas) can have negative effects on other industries, because resources are taken away from other sectors. Heavily investing in gas came at the expense of less output in manufacturing.
Higher taxes and public spending
At first glance the public purse may appear to be a zero-sum game. If the government spend more on education, there is an opportunity cost of higher taxes and/or lower spending elsewhere. However, spending more on education is not necessarily a zero-sum game. If government spending increases educational standards, then workers will become more productive and this will increase economic growth and lead to higher tax revenues. Therefore over time, the higher spending on education will pay dividends of increased tax revenue and better educated workforce. Therefore, the decision to shift spending to education is not a purely zero-sum game because there are knock-on benefits. The aggregate benefits are greater than the aggregate losses.
The cognitive bias of Zero-sum games
We are accustomed to thinking in terms of zero-sum games. We tend to think of situations as zero-sum. For example, if immigrants enter the country, a response may be to think the immigrants will take our jobs and reduce wages. However, this is a fallacy. (known as lump of labour fallacy). Because immigrants do take jobs, but equally create new demand for labour. Supply of labour increases but so does demand.
The opposite of zero-sum thinking could be said to be ‘abundance mentality’
For example, should women’s wages be increased to be on par with men?
At first glance, a man might fear that increasing women’s wages would be at the expense of men. A zero-sum game women catch up with men, men’s wages fall. However, it may be likely that women’s wages can be increased without cutting men’s wages.
- Women may be more motivated with equal pay, labour productivity increases
- With more income, women will buy more, increasing demand for labour.